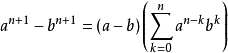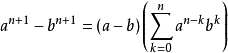O'Stolz定理是处理数列不定式极限的有力工具,一般用于*/∞型的极限(即分母趋于正无穷大的分式极限,分子趋不趋于无穷大无所谓)、0/0型极限(此时要求分子分母都以0为极限)。O'Stolz定理用于数列,它有函式形式的推广,这两个都可以认为是洛必达法则的离散版本。
基本介绍
- 中文名:O'Stolz定理、施笃兹定理、施托尔兹定理
- 外文名:The O'Stolz theorem
- 性质:定理
- 学科:数学
- 用于:不定式数列极限
定理简介
(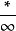 型) 设数列
型) 设数列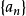 、
、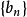 满足:①
满足:①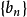 严格单调递增 ②
严格单调递增 ②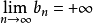 ③
③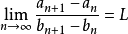 (其中
(其中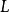 可以为有限实数、
可以为有限实数、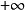 、
、 )
)
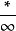
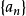
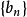
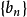
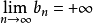
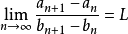
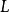
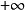

则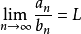
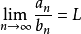
这个是较常用的版本
( 型) 设数列
型) 设数列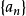 、
、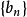 满足:①
满足:①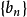 严格单调递减且趋于零 ②
严格单调递减且趋于零 ②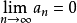 ③
③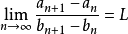 (其中
(其中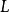 可以为有限实数、
可以为有限实数、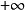 、
、 )
)

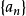
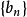
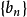
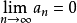
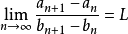
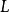
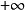

则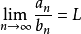
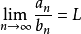
证明过程
一、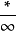 型
型
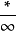
(当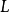 为有限实数时)由
为有限实数时)由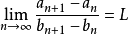 ,
,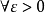 ,
,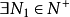 ,当
,当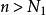 时,
时,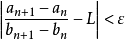 , 即
, 即
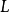
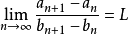
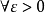
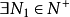
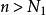
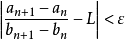
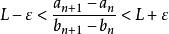

(这里可以把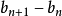 乘到不等号另一边是因为
乘到不等号另一边是因为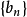 严格单调递增,所以
严格单调递增,所以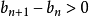 ,乘到不等号另一边时不变号)
,乘到不等号另一边时不变号)
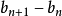
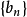
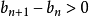
又由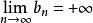 ,∴
,∴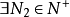 ,当
,当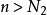 时,
时,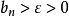 (这里是根据数列趋于正无穷大的定义),∴
(这里是根据数列趋于正无穷大的定义),∴ (注一)
(注一)
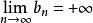
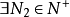
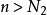
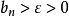

取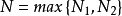 ,当
,当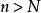 时,从
时,从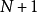 到
到 对
对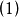 式累加,有
式累加,有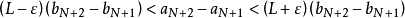
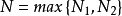
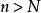
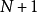

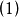
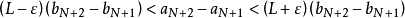
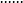
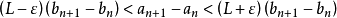
累加得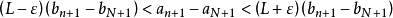
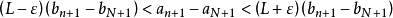
同除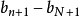 (还是因为
(还是因为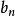 严格单调递增,
严格单调递增,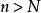 ,
,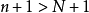 ,
,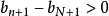 ),还注意到
),还注意到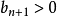 ,因为
,因为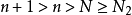 ,
,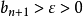
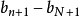
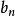
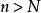
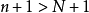
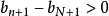
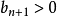
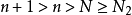
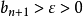
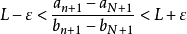
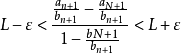
即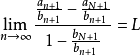 ,由
,由 ,且
,且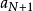 、
、 是常数,因为
是常数,因为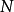 是确定的下标!由极限的四则运算法则,
是确定的下标!由极限的四则运算法则,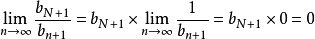 (注二),
(注二),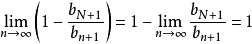 ,同理
,同理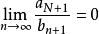 ,再由极限的四则运算法则,
,再由极限的四则运算法则,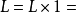
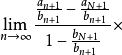
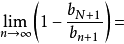
 ,
,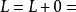
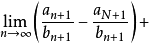
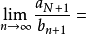
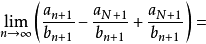
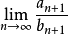 [1]
[1]
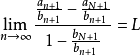

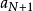

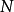
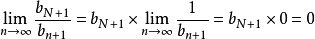
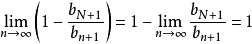
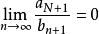
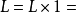
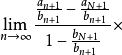
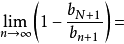

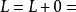
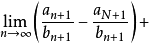
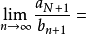
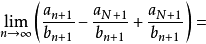
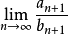
即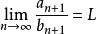 ,
,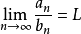
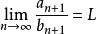
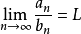
__________________________________________________________________________________________
为了方便初学者,这里解释一下以上的跳步。注意以下的注里出现的符号与上面证明的符号是分开的!比如注一的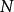 与证明里的
与证明里的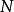 不同啊,初学者不要搞混。
不同啊,初学者不要搞混。
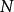
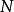
注一:我们可以证明,若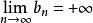 ,则
,则 ,
,
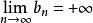

证明:由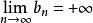 ,
,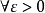 ,
,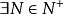 ,当
,当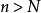 时,
时,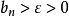 ,
,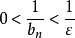 ,∴
,∴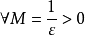 ,
,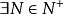 ,当
,当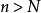 时,
时,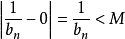 ,即
,即
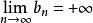
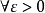
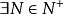
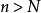
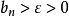
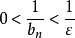
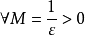
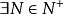
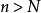
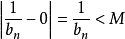

注二:由注一, ,可推出
,可推出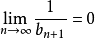 ,相当于去掉了第一项,然而极限是趋于无穷的行为,有没有这一点对极限毫无影响,后面的
,相当于去掉了第一项,然而极限是趋于无穷的行为,有没有这一点对极限毫无影响,后面的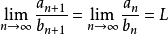 也是如此,当然这一点是可以证明的,这里略去。可以看[2]的第4题的证明过程。
也是如此,当然这一点是可以证明的,这里略去。可以看[2]的第4题的证明过程。

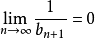
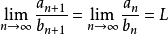
还有倒数第二段那里一堆的使用极限四则运算法则,严谨性是达到了,为了初学者能正确掌握,但是看起来很繁琐,其实这段里面的一些步骤在已经学了数学分析的同学眼里是已知的,无须写出来的。所以如果你要在正式场合写该定理的证明,以上证明中的"因为"后面的解释说明和倒数第二段的繁杂过程可以删减,按你的意愿做相应简化即可。
一个例子
例:求极限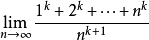 (k为正整数)。
(k为正整数)。
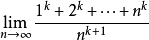
解:令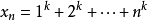 ,
,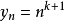
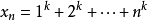
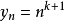
由O'Stolz定理
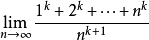
=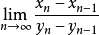 =
=
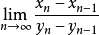

注: