为了分析语音信号而提出的一个算法模型.在语音信号处理上用的比较多

隐马尔可夫模型（HMMs）是对语音信号的时间序列结构建立统计模型，可将之看作一个数学上的双重随机过程：一个是用具有有限状态数的Markov链来模拟语音信号统计特性变化的隐含的随机过程，另一个是与Markov链的每一个状态相关联的观测序列的随机过程。前者通过后者表现出来，但前者的具体参数是不可测的。人的言语过程实际上就是一个双重随机过程，语音信号本身是一个可观测的时变序列，是由大脑根据语法知识和言语需要(不可观测的状态) 发出的音素的参数流。可见HMM合理地模仿了这一过程，很好地描述了语音信号的整体非平稳性和局部平稳性,是较为理想的一种语音模型。从整段语音来看，人类语音是一个非平稳的随机过程，但是若把整段语音分割成若干短时语音信号，则可认为这些短时语音信号是平稳过程，我们就可以用线性手段对这些短时语音信号进行分析。若对这些语音信号建立隐马尔可夫模型，则可以辩识具有不同参数的短时平稳的信号段，并可以跟蹤它们之间的转化，从而解决了对语音的发音速率及声学变化建立模型的问题。

HMMS(HyperMedia Management Schema) WBEM的一部分

是一种可扩展的，独立于实现的公共数据描述模式。它能够描述，实例化和访问各种数据，是对各种被管对象的高层抽象。它由核心模式和特定域模式两层构成，核心模式由高层的类以及属性 关联组成、将被管理环境分成被管系统元素、套用部件和网路部件。特定域模式继承了核心模式，採用其基本的语义定义某一特定环境的对象。

在一个环环相扣的随机变数的序列中，每个随机变数以多大的机率取什幺值，仅仅与它前面一个变数有关，而与它更前面的变数无关。

在已知“现在”的的条件下，“未来”与“过去”彼此独立的特性就被称为马尔科夫性，具有这种性质的随机过程就叫做马尔科夫过程，其最原始的模型就是马尔科夫链。

用一个通俗的比喻来形容，一只被切除了大脑的白鼠在若干个洞穴间的蹿动就构成一个马尔科夫链。因为这只白鼠已没有了记忆，瞬间而生的念头决定了它从一个洞穴蹿到另一个洞穴；当其所在位置确定时，它下一步蹿往何处与它以往经过的路径无关。这一模型的哲学意义是十分明显的，用前苏联数学家辛钦（1894－1959〕的话来说，就是承认客观世界中有这样一种现象，其未来由现在决定的程度，使得我们关于过去的知识丝毫不影响这种决定性。

隐马尔可夫模型由五个要素组成，其中两个状态集合（N、M），三个机率矩阵（A、B、π）：

1）N，表示模型中的状态数，状态之间可以相互转移。

2）M，表示每个状态不同的观察符号，即输出字元的个数。

3）A，状态转移机率分布。

4）B，观察符号在各个状态下的机率分布。

5）π，表示初始状态分布。

给定N,M,A,B, π,HMMs能够输出一个观察符号序列，这个序列的元素属于M。

因为隐马尔可夫模型由两个状态集合和三个机率矩阵构成，所以HMMs可以形式化定义为一个五元组（N，M，A，B，π）。

输入：HMMs的五元组（N，M，A，B，π）。

输出：一个观察符号的序列，这个序列的每个元素都是M中的元素。

一个隐士也许不能够直接获取到天气的观察情况，但是他有一些水藻。民间传说告诉我们水藻的状态与天气状态有一定的机率关係——天气和水藻的状态是紧密相关的。在这个例子中我们有两组状态，观察的状态（水藻的状态）和隐藏的状态（天气的状态）。我们希望为隐士设计一种算法，在不能够直接观察天气的情况下，通过水藻和马尔科夫假设来预测天气。

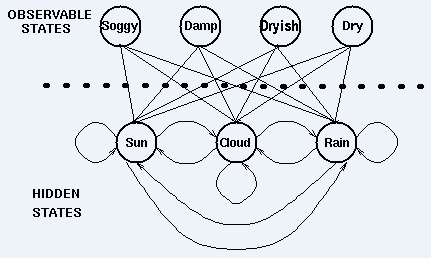
例子中，需要着重指出的是，隐藏状态的数目与观察状态的数目可以是不同的。一个包含三个状态的天气系统（晴天、多云、雨天）中，可以观察到4个等级的海藻湿润情况（乾、稍乾、潮湿、湿润）。

在这种情况下，观察到的状态序列与隐藏过程有一定的机率关係。我们使用隐马尔科夫模型对这样的过程建模，这个模型包含了一个底层隐藏的随时间改变的马尔科夫过程，以及一个与隐藏状态某种程度相关的可观察到的状态集合。

下图显示的是天气例子中的隐藏状态和观察状态。假设隐藏状态（实际的天气）由一个简单的一阶（即只与前一个变数有关）马尔科夫过程描述，那幺它们之间都相互连线。隐藏状态和观察状态之间的连线表示：在给定的马尔科夫过程中，一个特定的隐藏状态生成特定的观察状态的机率。这很清晰的表示了‘进入’一个观察状态的所有机率之和为1，在上面这个例子中就是Pr(Obs|Sun), Pr(Obs|Cloud) 及 Pr(Obs|Rain)之和。

除了定义了马尔科夫过程的机率关係，我们还有另一个矩阵，定义为混淆矩阵（confusion matrix），它包含了给定一个隐藏状态后得到的观察状态的机率。对于天气例子，混淆矩阵是：

注意矩阵的每一行之和是1。

我们已经看到在一些过程中一个观察序列与一个底层马尔科夫过程是机率相关的。在这些例子中，观察状态的数目可以和隐藏状态的数码不同。
我们使用一个隐马尔科夫模型（HMM）对这些例子建模。这个模型包含两组状态集合和三组机率集合：
* 隐藏状态：一个系统的（真实）状态，可以由一个马尔科夫过程进行描述（例如，天气）。
* 观察状态：在这个过程中‘可视’的状态（例如，海藻的湿度）。
*pi向量：包含了（隐）模型在时间t=1时一个特殊的隐藏状态的机率（初始机率）。
* 状态转移矩阵：包含了一个隐藏状态到另一个隐藏状态的机率
* 混淆矩阵：包含了给定隐马尔科夫模型的某一个特殊的隐藏状态，观察到的某个观察状态的机率。
因此一个隐马尔科夫模型是在一个标準的马尔科夫过程中引入一组观察状态，以及其与隐藏状态间的一些机率关係。

假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什幺.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什幺事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况.

你认为天气的运行就像一个马尔可夫链.其有两个状态 "雨"和"晴",但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的机率进行下列活动:"散步", "购物", 或 "清理". 因为你朋友告诉你他的活动,所以这些活动就是你的观察数据.这整个系统就是一个隐马尔可夫模型HMM.

你知道这个地区的总的天气趋势,并且平时知道你朋友会做的事情.也就是说这个隐马尔可夫模型的参数是已知的.你可以用程式语言(Python)写下来:

states = ('Rainy', 'Sunny') #模型中的状态集合N observations = ('walk', 'shop', 'clean') #每个状态不同的观察符号Mstart_probability = {'Rainy': 0.6, 'Sunny': 0.4} #初始状态分布π#状态转移机率分布Atransition_probability = { 'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3}, 'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6}, } #观察符号在各个状态下的机率分布Bemission_probability = { 'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5}, 'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1}, }

在这些代码中,start_probability代表了你对于你朋友第一次给你打电话时的天气情况的不确定性(你知道的只是那个地方平均起来下雨多些).在这里,这个特定的机率分布并非平衡的,平衡机率应该接近（在给定变迁机率的情况下）{'Rainy': 0.571, 'Sunny': 0.429}<transition_probability表示基于马尔可夫链模型的天气变迁,在这个例子中,如果今天下雨,那幺明天天晴的机率只有30%.代码emission_probability表示了你朋友每天做某件事的机率.如果下雨,有 50% 的机率他在清理房间;如果天晴,则有60%的机率他在外头散步.

一旦一个系统可以作为HMM被描述，就可以用来解决三个基本问题。其中前两个是模式识别的问题：给定HMM求一个观察序列的机率（评估）；搜寻最有可能生成一个观察序列的隐藏状态序列（解码）。第三个问题是给定观察序列生成一个HMM（学习）。

1） 评估，考虑这样的问题，我们有一些描述不同系统的HMMs及一个观察序列。我们想知道哪一个HMMs模型最有可能产生这个给定的观察序列。也就是通过HMMs来求给定序列的机率，哪个机率大，我们就认为是哪个HMMs。

2） 解码，这个问题是我们最感兴趣的，因为，我们对隐藏状态序列更加感兴趣，所以，我们想通过给定的HMMs模型及观察序列来确定隐藏状态序列。

3） 学习，这个问题是最难的，根据观察序列以及一个隐藏状态集合，来估计一个最合适的HMMs模型，当状态转移矩阵和混淆矩阵不能被直接测量时，我们可以用向前向后算法来估计参数。

由一个向量和两个矩阵(pi，A，B)描述的隐马尔可夫模型对于实际系统有着巨大的价值，虽然经常只是一种近似，但他们是经得起分析的，HMMs通常解决的问题有：

1） 对于一个观察序列匹配一个最可能的系统----评估，使用向前算法（forward algorithm）解决。

2） 对于已生成的观察序列，确定最可能的隐藏状态序列----解码，使用维特比算法（Viterbi algorithm）解决。

3） 对于已有的观察序列，决定最有可能的模型参数----学习，使用向前向后算法(forward backward algorithm)解决。

HMMs的缺点：HMMs的一些假设过于简单。