Gell-Mann矩阵实际就是上是SU(3)群特定选取的一组生成元(李代数)的特定基础表示。所谓“特定选取”是指这些矩阵的正交性(至多差一个归一化因子)。也就是说以这些特定矩阵为基的SU(3)伴随表示是幺正的。“特定基础表示”是由于物理学家约定了一种常用的表示,而不是其他等价表示。Gell-Mann矩阵是为了分析强相互作用味对称性而提出的(u,d,s夸克之间的SU(3)对称性),广泛套用于强子分类。而之后物理学家们在分析其他SU(3)对称性时都会选取这种表示(比如色的SU(3)对称性)。
基本介绍
- 中文名:Gell-Mann矩阵
- 外文名:Gell-Mann matrices
定义
在利用强相互作用SU(3)味对称性进行强子分类时,Gell-Mann所提出的SU(3)群特定选取的一组生成元(李代数)的特定基础表示,这种矩阵表示被称为Gell-Mann矩阵。具体定义见图1:
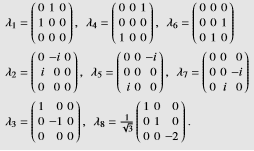
SU(3)的生成元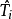 (基础表示)定义为:
(基础表示)定义为:
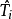
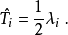
所谓“特定选取”是指矩阵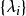 的正交性(至多差一个归一化因子)。也就是说以这些特定矩阵为基的SU(3)伴随表示是幺正的。“特定基础表示”是由于物理学家约定了一种常用的表示,而不是其他等价表示。
的正交性(至多差一个归一化因子)。也就是说以这些特定矩阵为基的SU(3)伴随表示是幺正的。“特定基础表示”是由于物理学家约定了一种常用的表示,而不是其他等价表示。
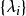
性质
在定义内积后,Gell-Mann矩阵具有正交性:
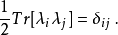
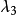
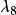
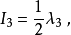
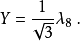
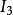
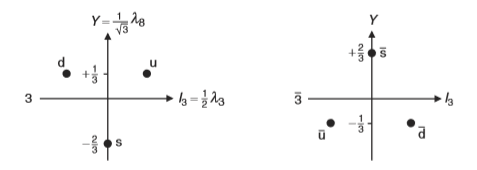 图2
图2物理中的套用
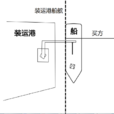
Gell-Mann矩阵在强子分类中有重大意义,可以看见图2中已经将u,d,s夸克及其对应的反夸克填入权图之中。一方面,数学上是由于Gell-Mann矩阵建立时,就是选取在以u,d,s为基的SU(3)的基础表示下;另一方面,我们也可以看出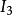 和
和 的物理意义。
的物理意义。
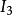

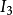
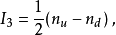
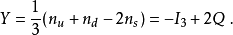
由3与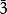 表示的直积化直和,生成伴随表示8,就可以给出对轻夸克组成的介子的8重态分类,具体见图3:
表示的直积化直和,生成伴随表示8,就可以给出对轻夸克组成的介子的8重态分类,具体见图3:
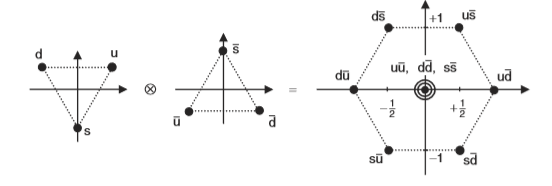 图3
图3发展历史
1961年盖尔曼在奇异数守恆定律的基础上,又提出了SU(3)对称性。对强相互作用的粒子进一步作出分类。效仿佛教的“八正道”(即“正见、正思维、正语、正业、正命、正精进、正念、正定”),1962年盖尔曼和以色列物理学家内曼(Y. Neemann)独立地提出了“八正法”的分类方法。他们假设,八个质量最小的重子;两个核子、三个Σ超子、两个E超子及一个∧超子,构成一个“超多重态”。这八个重子,自旋都是1/2,宇称均为正值,质量相近。只是电荷不同、同位旋不同、奇异数不同。因此可以画一个超荷Y和同位旋分量I3的坐标图,二重态、三重态和单态可以排成一个整齐的六边形列阵。
盖尔曼打算用八正方法把所有新的粒子和新的量子数都综合进来。按照这一方法,还可以把当时已知的九个重子共振态排列成对称的图形。从这张图形的对称性考虑,似乎缺少了一个粒子,这个粒子的特性可以从图形的对称性推出。1962年盖尔曼在欧洲核予研究中心的会议上提出这个失蹤的粒子应该具有电荷为一1,奇异数为一3,质量为1680兆电子伏,自旋为3/2,字称为正值。1964年果然发现了Ω粒子正是这个失蹤的粒子。这样就对盖尔曼的八正方法作出了有力的支持。