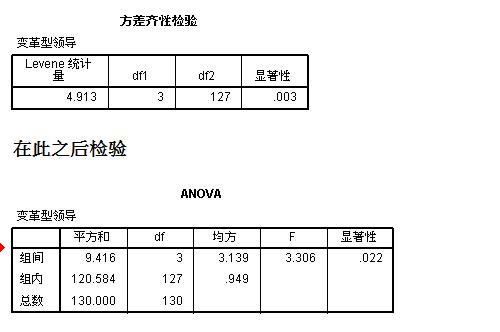
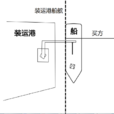
F检验（F-test），最常用的别名叫做联合假设检验（英语：joint hypotheses test），此外也称方差比率检验、方差齐性检验。它是一种在零假设（null hypothesis, H0）之下，统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型，以判断该模型中的全部或一部分参数是否适合用来估计母体。
F检验这名称是由美国数学家兼统计学家George W. Snedecor命名，为了纪念英国统计学家兼生物学家罗纳德·费雪（Ronald Aylmer Fisher）。Fisher在1920年代发明了这个检验和F分配，最初叫做方差比率（Variance Ratio）。
基本介绍
- 中文名：F检验
- 外文名：F-test
- 全称：方差齐性检验
- 用途：在两样本t检验中要用到
- 提出者：英国统计学家Fisher
- 别名：方差比率
- 套用学科：统计学
计算
样本标準偏差的平方，即：
S2=∑(
-
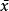)2/(n-1)
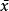
两组数据就能得到两个S2值
F=S2/S2'
然后计算的F值与查表得到的F表值比较，如果
F < F表 表明两组数据没有显着差异；
F ≥ F表 表明两组数据存在显着差异。
表格
置信度95%时F值(单边)
f大 f小 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ∞ |
2 3 4 5 6 7 8 9 10 ∞ | 19.0 9.55 6.94 5.79 5.14 4.74 4.46 4.26 4.10 3.00 | 19.16 9.28 6.59 5.41 4.76 4.35 4.07 3.86 3.71 3.60 | 19.25 9.12 6.39 5.19 4.53 4.12 3.84 3.63 3.48 2.37 | 19.30 9.01 6.26 5.05 4.39 3.97 3.69 3.48 3.33 3.21 | 19.33 8.94 6.16 4.95 4.28 3.87 3.58 3.37 3.22 2.10 | 19.36 8.88 6.09 4.88 4.21 3.79 3.50 3.29 3.14 2.01 | 19.37 8.84 6.04 4.82 4.51 3.73 3.44 3.23 3.07 1.94 | 19.38 8.81 6.00 4.78 4.10 3.68 3.39 3.18 3.02 1.88 | 19.39 8.78 5.96 4.74 4.06 3.63 3.34 3.13 2.97 1.83 | 19.5 8.53 5.63 4.36 3.67 3.23 2.93 2.71 2.54 1.00 |
横向为大方差数据的自由度；纵向为小方差数据的自由度。
适用场合
通常的F检验例子包括：
- 假设一系列服从常态分配的母体，都有相同的标準差。这是最典型的F检验，该检验在方差分析（ANOVA）中也非常重要。
- 假设一个回归模型很好地符合其数据集要求。
注意事项
F检验对于数据的正态性非常敏感，因此在检验方差齐性的时候，Levene检验, Bartlett检验或者Brown–Forsythe检验的稳健性都要优于F检验。 F检验还可以用于三组或者多组之间的均值比较，但是如果被检验的数据无法满足均是常态分配的条件时，该数据的稳健型会大打折扣，特别是当显着性水平比较低时。但是，如果数据符合常态分配，而且alpha值至少为0.05，该检验的稳健型还是相当可靠的。
若两个母体有相同的方差（方差齐性），那幺可以採用F检验，但是该检验会呈现极端的非稳健性和非常态性，可以用t检验、巴特勒特检验等取代。
关係
- F检验的分子、分母其实各是一个卡方变数除以各自的自由度。
- F检验用来检验单一变数可否排除于模型外时， F=t2。
