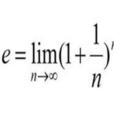自然常数,是数学中一个常数,是一个无限不循环小数,且为超越数,其值约为2.71828。
基本介绍
- 中文名:自然常数
- 外文名:e
- 本质:一个无限不循环数,超越数
- 大小:约为2.718281828
起源
e,作为数学常数,是自然对数函式的底数。有时称它为欧拉数(Euler number),以瑞士数学家欧拉命名;也有个较鲜见的名字纳皮尔常数,以纪念苏格兰数学家约翰·纳皮尔 (John Napier)引进对数。它就像圆周率π和虚数单位i,e是数学中最重要的常数之一。
它的其中一个定义是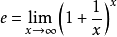 ,其数值约为(小数点后100位):“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。
,其数值约为(小数点后100位):“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。
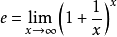
第一次提到常数e,是约翰·纳皮尔(John Napier)于1618年出版的对数着作附录中的一张表。但它没有记录这常数,只有由它为底计算出的一张自然对数列表,通常认为是由威廉·奥特雷德(William Oughtred)製作。第一次把e看为常数的是雅各·伯努利(Jacob Bernoulli)。
已知的第一次用到常数e,是莱布尼茨于1690年和1691年给惠更斯的通信,以b表示。1727年欧拉开始用e来表示这常数;而e第一次在出版物用到,是1736年欧拉的《力学》(Mechanica)。虽然以后也有研究者用字母c表示,但e较常用,终于成为标準。
用e表示的确实原因不明,但可能因为e是“指数”(exponential)一字的首字母。另一看法则称a,b,c和d有其他经常用途,而e是第一个可用字母。不过,欧拉选这个字母的原因,不太可能是因为这是他自己名字Euler的首字母,因为他是个很谦虚的人,总是恰当地肯定他人的工作。
以e为底的指数函式的重要方面在于它的函式与其导数相等。e是无理数和超越数(见林德曼—魏尔施特拉斯定理(Lindemann-Weierstrass))。这是第一个获证的超越数,而非故意构造的(比较刘维尔数);由夏尔·埃尔米特(Charles Hermite)于1873年证明。
其实,
超越数主要只有自然常数(e)和圆周率(π)。自然常数的知名度比圆周率低很多,原因是圆周率更容易在实际生活中遇到,而自然常数在日常生活中不常用。
融合e,π的的欧拉公式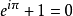 ,也是超越数e的数学价值的最高体现。
,也是超越数e的数学价值的最高体现。
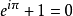
自然常数一般为公式中乘方的底数和对数的底。为什幺会这样,主要取决于它的来历。
自然常数的来法比圆周率简单多了。它就是当 时函式
时函式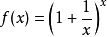 值的极限。
值的极限。

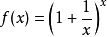
即: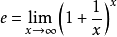 。
。
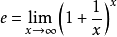
同时,它也等于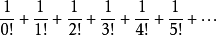 。注意,
。注意,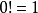 。
。
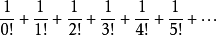
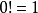
自然常数经常在公式中做对数的底。比如,对指数函式和对数函式求导时,就要使用自然常数。函式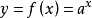 的导数为
的导数为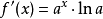 。函式
。函式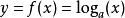 的导数为
的导数为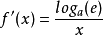 。
。
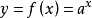
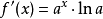
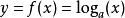
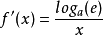
因为e=2.7182818284... ,极为接近循环小数2.71828(1828循环),那就把循环小数化为分数271801/99990,所以可以用271801/99990表示为e最接近的有理数约率,精确度高达99.9999999(7个9)% 。
收敛性证明
由均值不等式,有
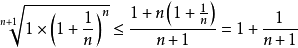
即序列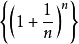 单调上升;另一方面,我们尝试证明
单调上升;另一方面,我们尝试证明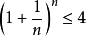 。即要证
。即要证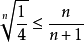 ,由均值不等式得
,由均值不等式得
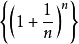
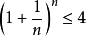
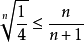
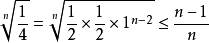
又明显有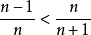 ,故
,故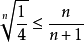 成立,所以
成立,所以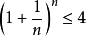 成立。
成立。
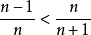
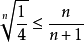
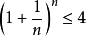
故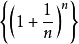 单调上升有上界,即
单调上升有上界,即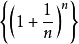 收敛。
收敛。
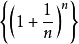
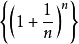
另外形式
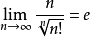
证法1
令 ,易知
,易知

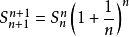
则已知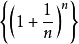 收敛于
收敛于 ,即
,即
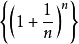

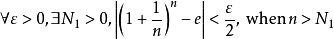
即
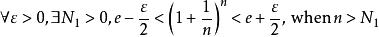
所以,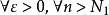 ,不妨设
,不妨设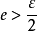 ,则有
,则有
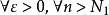
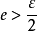
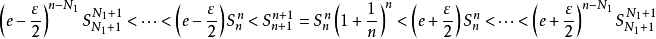
即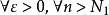 ,有
,有
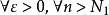
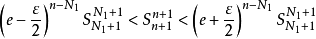
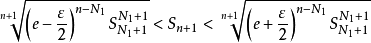
又易知对固定的 和
和 ,有
,有


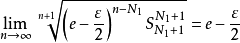
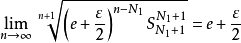

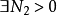
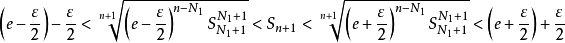
即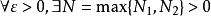 ,当 时,有
,当 时,有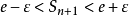 ,即
,即
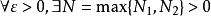
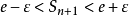
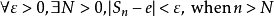
即
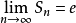
注:由该证法可以看出,对任意正数序列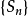 ,若存在一个收敛数列
,若存在一个收敛数列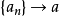 ,使得
,使得
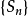
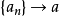

则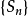 收敛,且极限为
收敛,且极限为 .
.
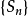

证法2
欲证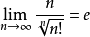 ,即要证
,即要证
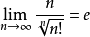
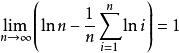
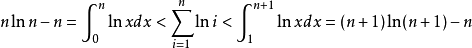
则有

故有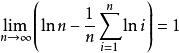
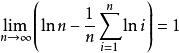
证毕.
计算方法
泰勒公式展开
已知函式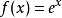 存在任意阶的导数。将其在点
存在任意阶的导数。将其在点 处进行泰勒展开,有
处进行泰勒展开,有
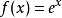

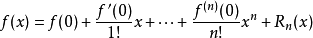
取Peano形式的余项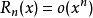
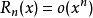
令上式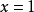 ,有
,有
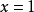
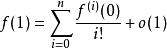
故有
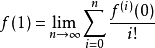
即得
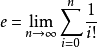
由此就可根据上式求解出 的具体数值
的具体数值

限制精度
但是在套用中我们需要的是 的具有某位精度的数值,比如说要求
的具有某位精度的数值,比如说要求 的小数点前2000位的準确数值。此时Peano余项不够用了。我们换一个余项,例如——Lagrange余项:
的小数点前2000位的準确数值。此时Peano余项不够用了。我们换一个余项,例如——Lagrange余项:


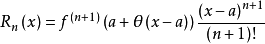
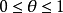
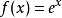
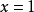
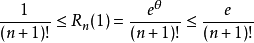
所以
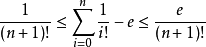
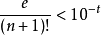


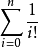
便得 的小数点后t位的準确数值
的小数点后t位的準确数值

套用
自然常数e在科学上有广泛套用。以下举几例:
1:e对于自然数的特殊意义
所有大于2的2n形式的偶数存在以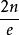 为中心的共轭奇数组,每一组的和均为2n,而且至少存在一组是共轭素数
为中心的共轭奇数组,每一组的和均为2n,而且至少存在一组是共轭素数
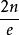
可以说 是素数的中心轴,
是素数的中心轴, 只是奇数的中心轴。
只是奇数的中心轴。


2:素数定理
自然常数也和质数分布有关。有某个自然数a,则比它小的质数就大约有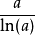 个。在a较小时,结果不太正确。但是随着a的增大,这个定理会越来越精确。这个定理叫素数定理,由高斯发现。
个。在a较小时,结果不太正确。但是随着a的增大,这个定理会越来越精确。这个定理叫素数定理,由高斯发现。
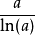
3:完全率
设完全图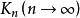 内的路径总数为W,哈密顿路总数为h,则W/h=e,此规律更证明了e并非故意构造的,e甚至也可以称呼为是一个完全率。与圆周率有一定的相类似性,好像极限完全图就是图论中的圆形,哈密顿路就是直径似的,自然常数的含义是极限完全图里的路径总数和哈密顿路总数之比。
内的路径总数为W,哈密顿路总数为h,则W/h=e,此规律更证明了e并非故意构造的,e甚至也可以称呼为是一个完全率。与圆周率有一定的相类似性,好像极限完全图就是图论中的圆形,哈密顿路就是直径似的,自然常数的含义是极限完全图里的路径总数和哈密顿路总数之比。
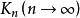
4:双曲函式
双曲函式是自然常数价值的重要体现。它可以解决很多问题。如:
阻力落体
在空气中由静止开始下落的小石块既受重力的作用又受到阻力的作用。设小石块的质量为m,速度为v,重力加速度为g,所受空气阻力假定与v2正比,阻尼係数为μ。设初始时刻小石块静止。求其小石块运动速度与时间的关係。[3]
解:
小石块遵循的运动方程为
mdv/dt=mg―μv2
(1)
这是Riccati方程,它可以精确求解。
依标準变换方式,设
v=(m/μ)/(z′/z) (2)
代入(1)式,再作化简,有
z'' ―(gμ /m)z=0 (3)
(3)式的通解是
z=C1exp(√gμ /m t)+ C2exp(-√gμ /m t)(4)
其中,C1和C2是任意常数。
由于小石块在初始时刻是静止的,初始条件为
v(0)=0 (5)
这等价于
z′(0)=0 (6)
因此,容易定出
C2=C1 (7)
将(7)式代入(4)式,再将(4)式代入(2)式,就可得
满足初始条件的解
v=√mg/μ tanh(√μg/m t) (8)
我们可以作一下定性的分析。小石块初始时刻静止。因此,随着时间增加,开始时小石块速度较小,小石块所受的阻力影响较小,此时,小石块与不受阻力的自由落体运动情况相类似,小石块加速度几乎是常数。反映在图1中,起始段t和v的关係是直线。当小石块速度很大时,重力相对于阻力来说可以忽略,阻力快速增加到很大的数值,导致小石块的速度几乎不再增加。此时,小石块加速度接近零,v几乎不随时间而变化。一段时间后,v相不多是一平行于t轴的直线。
粒子运动
一电荷量为q、静质量为m0的粒子从原点出发,在一均匀电场E中运动,E=Eez沿z轴方向,粒子的初速度沿y轴方向,试证明此粒子的轨迹为[4]
x=(W0/qE)[cosh(qEy/p0c)―1] (1)
式中p0是粒子出发时动量的值,W0是它出发时的能量。
解:
带有电荷量q的粒子在电磁场E和B中的相对论性的运动方程为
dp/dt=q(E+v×B) (2)
式中v是粒子的速度,p是粒子的动量
p=mv=mv0/√1-v2/c2 (3)
本题运动方程的分量表示式为
dpx=qE
dpy=0
dpz=0 (4)
解之,有
px =qEt+C1
py = C2
pz = C3 (5)
代入t=0时初始条件
px(0)=0
py(0)= p0
pz(0)= 0 (6)
定出积分常数后,可知
px=qEt
py= p0
pz= 0 (7)
粒子的能量为
W=mc2
=√p2c2+m02c4
=√(px2+ py2+ pz2)c2+m02c4
=√q2E2 c2t2+W02 (8)
因dx/dt=qEt/m=qEc2t/√q2E2 c2t2+W02 (9)
积分得
x=∫[qEc2t/√q2E2 c2t2+W02 ]dt
= [√q2E2 c2t2+W02 -W02]/qE (10)
又由(7)式得
dy/dt=p0/m=p0c2/√q2E2 c2t2+W02 (11)
积分得
y=∫[p0c2 /√q2E2 c2t2+W02 ]dt
=(p0c /qE)arsh(qEct/W0) (12)
或 (qEct/W0)= sinh (qEy/ p0c) (13)
在(51)式和(54)式中消去t,有
x=(W0/qE)[√1+ sinh2(qEy/ p0c)-1 ] (14)
利用恆等变换公式
cosh2x―sinh2x=1 (15)
(55)式可以写成
x=(W0/qE)[cosh2(qEy/ p0c)-1 ] (16)
(16)式是一种悬链线。
讨论:
因双曲余弦泰勒级数展开式是
cosh(x)=1+x2/2!+x4/4!+x6/6!+…… (17)
当v/c →0时,保留前2项,得
x=(qE/2m v02)y2 (18)
(18)式是抛物线轨迹。《普通物理学》教材用经典牛顿力学求解,普遍会给有这个结果。这表示,非相对论确是相对论在v/c →0时的极限。或者说,(18)式成立的条件是v/c<<1,这也是牛顿力学的适用範围。