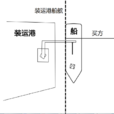
在量子力学里，Delta位势垒是一个垒内位势为狄拉克Delta函式，垒外位势为0的位势垒。Delta位势垒问题专门研讨，在这种位势的作用中，一个移动的粒子的量子行为。我们想要知道的是，在被Delta位势垒散射的状况下，粒子的反射係数与透射係数。在许多量子力学的教科书里，这是一个常见的习题。
基本介绍
- 中文名：Delta位势垒
- 外文名：Delta potential
- 领域：量子力学
定义
一个粒子独立于时间的薛丁格方程为
图1.对于一个Delta位势垒的散射
图1.对于一个Delta位势垒的散射
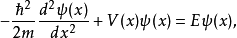
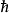
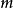
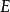
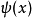
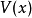
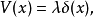
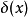
导引
这位势垒将一维空间分为两个区域：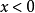
与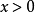
。在任何一个区域内，位势为常数，薛丁格方程的解答可以写为往右与往左传播的波函式的叠加（参阅自由粒子）：
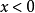
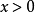
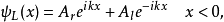
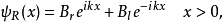
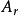
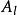
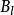
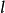
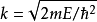
由于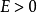
，
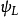与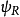
都是行进波。这两个波必须满足在
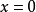的边界条件：
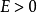
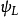
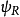
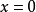
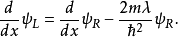
特别注意第二个边界条件方程，波函式随位置的导数在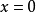
并不是连续的，在位势垒两边的差额有
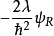这幺多。这方程的推导必须用到薛丁格方程。将薛丁格方程积分于{\displaystyle x=0\,\!}的一个非常小的邻域：
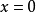
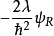
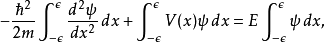
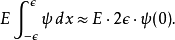
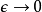
左边是
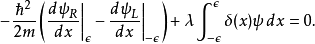
根据狄拉克Delta函式的定义，
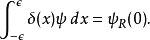
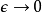
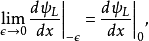
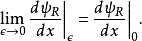
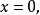
从这两个边界条件方程。稍加运算，可以得到以下方程：
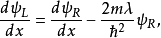
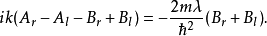
反射与透射
由于能量是正值的，粒子可以自由的移动于位势垒外的两个半空间，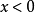
或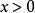
。可是，在Delta位势垒，粒子会遇到散射状况。设定粒子从左边入射。在Delta位势垒，粒子可能会被反射回去，或者会被透射过去。我们想要知道散射的反射係数与透射係数。设定
，
，
，
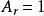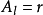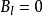。求算反射的机率幅
与透射的机率幅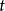
：
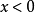
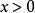
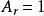
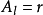
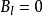
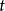
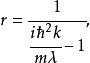
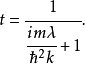
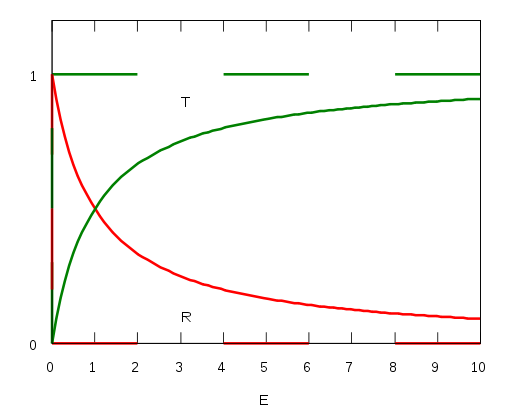
反射係数是
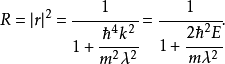
透射係数是
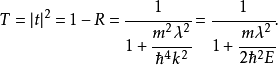
这纯粹是一个量子力学的效应，称为量子隧穿效应；在经典力学里，透射係数等于0，粒子不可能会透射过位势垒。
- 由于模型的对称性，假若，粒子从右边入射，我们也会得到同样的答案。
- 很奇异地，给予同样的能量、质量、与狄拉克Delta函式的强度，Delta位势垒与Delta位势阱有同样的反射係数与透射係数。
参阅
- 自由粒子
- 无限深方形阱
- 有限深方形阱
- 有限位势垒
- 球对称位势
- Delta位势阱
- 量子隧穿效应
