COX回归模型，又称“比例风险回归模型(proportional hazards model，简称Cox模型)”，是由英国统计学家D.R.Cox(1972)年提出的一种半参数回归模型。该模型以生存结局和生存时间为应变数，可同时分析众多因素对生存期的影响，能分析带有截尾生存时间的资料，且不要求估计资料的生存分布类型。由于上述优良性质，该模型自问世以来，在医学随访研究中得到广泛的套用，是迄今生存分析中套用最多的多因素分析方法。
基本介绍
- 中文名：COX回归模型
- 外文名：Cox regression model
- 全称：Cox比例风险回归模型
- 提出人：D.R.Cox
- 简称：Cox模型
基本概念
在介绍Cox回归模型之前，先介绍几个有关的概念。
1.生存函式具有变数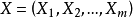
的观察对象的生存时间
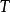大于某时刻
的机率，
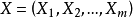
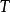
2. 死亡函式具有变数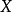
的观察对象的生存时间
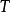不大于某时刻的机率，
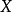
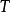
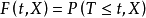
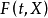
3. 死亡密度函式具有变数X的观察对象在某时刻t的瞬时死亡率，称为死亡密度函式。
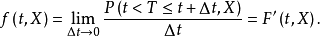
4. 危险率(风险)函式具有变数X，且生存时间已达到
的观察对象在时刻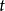
的瞬时死亡率，
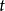
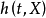
基本原理
生存分析的主要目的在于研究变数X与观察结果即生存函式(累积生存率)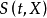
之间的关係。当 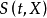受很多因素影响，即
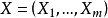为向量时，传统的方法是考虑回归方程——即诸变数
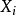对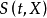 的影响。但由于生存分析研究中的数据包含删失数据。且时间变数t通常不满足常态分配和方差齐性的要求，这就造成了用一般的回归方法研究上述关係的困难。
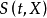
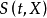
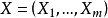
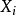
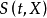
Cox回归模型的基本形式
D.R.Cox提出了Cox比例风险回归模型，它不是直接考察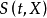 与X的关係，而是用
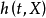作为因变数，模型的基本形式为：
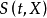
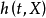
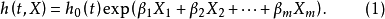
式中，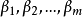
为自变数的偏回归係数，它是须从样本数据作出估计的参数；
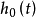是当X向量为0时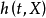， 的基準危险率，它是有待于从样本数据作出估计的量。公式(1)简称为Cox回归模型。
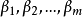
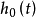
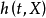
由于Cox回归模型对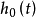 未作任何假定，因此Cox回归模型在处理问题时具有较大的灵活性；另一方面，在许多情况下，我们只需估计出参数
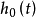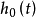(如因素分析等)，即使在 未知的情况下，仍可估计出参数 。这就是说，Cox回归模型由于含有 ，因此它不是完全的参数模型，但仍可根据公式(1)作出参数 的估计，故Cox回归模型属于半参数模型。
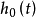
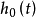
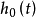
公式(1)可以转化为：
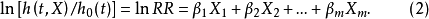
Cox回归模型的假定
1. 比例风险假定 各危险因素的作用不随时间的变化而变化，即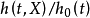
不随时间的变化而变化。因此，公式(1)又称为比例风险率模型(PH Model)。这一假定是建立Cox回归模型的前提条件。
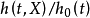
2．对数线性假定 模型中的协变数应与对数风险比呈线性关係，如公式(2)。
Cox回归模型中偏回归係数的意义
若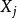
是非暴露组观察对象的各因素取值，
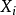是暴露组观察对象的各因素取值，由公式(3)就可以求出暴露组对非暴露组的相对危险度RR。
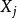
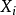
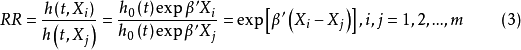
由公式(2)可见，模型中偏回归係数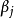
的流行病学含义是在其他协变数不变的情况下，协变数
每增加一个测定单位时所引起的相对危险度的自然对数的改变数。即
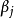
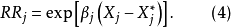
式中，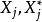
分别表示在不同情况下的取值。当协变数 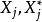分别取1和0时，其对应的
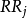为
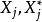
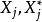
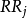
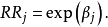
从公式(1)和公式(4)可以看出有如下关係：
若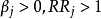
，则各
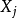取值越大时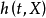， 的值越大，即 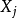为危险因素。
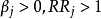
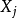
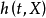
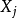
若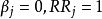
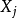，则各 的取值对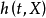 的值没有影响，即 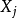为无关因素。
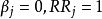
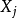
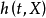
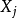
若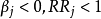
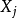，则各 取值越大时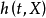， 的值越小，即 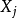为保护因素。
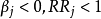
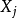
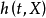
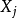
假设检验
Cox回归模型中的偏回归係数可以通过建立偏似然函式，利用Newton-Raphson叠代法求得。其他自变数不变的情况下，变数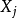 每增加一个单位，相对危险度 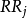的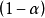
可信区间为：
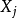
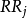
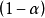
式中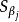
为
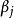的标準误。
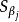
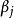
对于回归模型的假设检验通常採用似然比检验、Wald检验和记分检验，其检验统计量均服从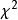
分布，其自由度为模型中待检验的自变数个数。一般说来，Cox回归係数的估计和模型的假设检验计算量较大，通常需利用计算机来完成相应的计算。
