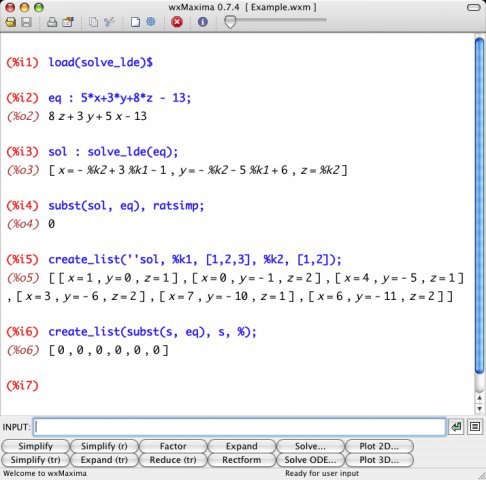
CAS是计算机代数系统(英文:Computer Algebra System)是进行符号运算的软体。这种系统的要件是数学表示式的符号运算。
基本介绍
- 中文名:计算机代数系统
- 外文名:CAS
表示式的类型
表示式的例子包括:
1.多变元多项式
2.标準函式(三角函式、指数函式等等)
3.特殊函式(Γ函式、Bessel函式等等)
4.由各种表示式合成的函式
5.表示式的导函式、积分、和与积
6.以表示式为係数的级数
7.表示式构成的矩阵
符号运算
以下是几种典型的符号运算:
1.表示式的简化
2.对表示式求值
3.表示式的变形:展开、积、幂次、部份分式表法、将三角函式表为指数函式等等。
4.对单变元或多变元的微分。
5.带条件或不带条件的整体最佳化。
6.部份或完整的因式分解。
7.求解线性方程组或一些非线性方程式。
8.某类微分方程或差分方程的符号解。
9.求某些函式的极限值。
10.一些函式的定积分或不定积分,包括多变元的情形。
11.泰勒展开式、罗朗展开式与Puiseux展开式
12.某些函式的无穷级数展开式。
13.对某些级数求和。
14.矩阵运算。
15.数学式的显示,通常借着TeX之类的系统达成。
其它功能
通常计算机代数系统还能进行一些数值运算:
1.函式的确切求值。
2.高精度求值,例如计算到小数点后位。
3.线性代数的数值运算。
4.描绘二维或三维的函式图形。
在数值运算方面,计算机代数系统的速度通常较Matlab、GNU Octave或C语言中以同等方式实现的程式慢。这是因为计算机系统几乎总是对符号表示式运算,故不能充分利用CPU的既有指令。
许多计算机代数系统内置高级程式语言,以供用户扩展,或设定个人的操作模式。
历史
马丁纽斯·韦尔特曼(Martinus J. G. Veltman) 是这个领域的先驱,他首先考虑了在高能物理中的套用。他在1963年设计的第一个程式叫Schoonship(荷兰文,意指“乾净的船”)。
最早受到欢迎的系统是Reduce、Derive与Macsyma,现在仍然可取得。Macsyma的一个GNU通用公共许可证发布的版本叫作Maxima,现在仍有维护。市场的龙头为Maple与Mathematica,两者被数学家、科学家及工程师们广泛採用,此外还有MuPAD与MathCad。
另有一些系统着眼于特定的套用领域,这些系统通常在学院中被设计、发展及维护,例如交换代数系统Macaulay 2或数论系统PARI/GP。
系统
mathHandbook.com (former symbmath)
Sagemath
Mathematica
Maple
MAGMA
Maxima
GAP
PARI/GP
Meditor
MuPAD
Mathomatic
Xcas / Giac
Yacas
Mate
标誌
计算机代数系统的标誌是能够以字元串作为运算单位。
不同的字元串代表的含义是不同的,字元串可以被赋值使它具有特殊含义。
例如:
a 作为一个字元串
b 作为另一个字元串
则有
2a 代表 2 乘以 a ,2个a的和。
a*b 代表 a 和 b 相乘。
ab 则代表另一个与 a 或 b 都不相关的字元串。
此时,给 a 赋值:2→a(令 a 等于 2)
则有
2a = 2*2 = 4
a*b = 2*b
ab 仍然是另一个独立的字元串。
ab * ab = 2*ab
(a*b)*(a*b) = a^2 * b^2 = 2^2 * b^2 = 4* b^2
特点
优点
1.可以进行符号运算,数值计算和图形显示,这是通用数学软体包的三大基本功能.具有高效的可程式功能.
2.多数计算机代数系统都是互动式的,人们通过键盘输入命令,计算机计算后显示结果.好的系统都有Windows作业系统下的版本,人机界面友好,命令输入方便灵活,很容易寻求帮助.结果的输出有多种形式,好的数学软体都提供了人们习惯的数学符号表达形式.
3.各个系统都在不断地发展完善,不断地更新换代,更新的速冻也在逐渐加快.数学软体在向着智慧型化,自动化方向发展.数学软体的实质是数学方法及其算法在计算机上的实现,这些方法是千百年来无数数学家的工作与智慧的结晶.
4.参与软体开发和套用的人员的数量在不断增加,而且日趋国际化.随着Internet的普及,软体用户可以很方便地与软体开发者进行沟通,反映软体中存在的问题,也把新的套用情况和好的程式提供给软体的开发者.软体的开发不再只是软体开发者的事情,也是广大用户的事情.
计算机代数系统的优越性主要在于它能够进行大规模的代数运算.通常我们用笔和纸进行代数运算只能处理符号较少的算式,当算式的符号上升到百位数后,手工计算便成为可能而不可行的事,主要原因是在做大量符号运算时,我们很容易出错,并且缺乏足够的耐心.当算式的符号个数上升到四位数后,手工计算便成为不可能的事,这时用计算机代数系统进行运算就可以做到準确,快捷,有效.
缺点
儘管计算机代数系统在代替人进行繁琐的符号运算上有着无比的优越性,但是,计算机毕竟是机器,它只能执行人们给它的指令.数学软体都有一定的局限性.首先,多数计算机代数系统对计算机硬体有较高的要求,在进行符号运算时,通常需要很大的记忆体和较长的计算时间,而精确的代数运算以时间和空间为代价的.一些人工计算的简单问题,计算机代数系统却做不出来.用数学软体的第二个问题是计算结果往往很长,人们很难从结果中看到问题的要害.用计算机代数系统进行数值计算,虽然计算精度可以到任意位,但由于计算机代数系统是用软体本身浮点运算代替硬体算术运算,所以在速度要比用Fortran语言算同样的问题慢百倍甚至千倍.另外,虽然计算机代数系统包含大量的数学知识,但这仅仅是数学的一小部分,目前有许多数学领域计算机代数系统还未能涉及.