Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续的回响变数不满足常态分配的情况。Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变数的相关性。Box-Cox变换的主要特点是引入一个参数,通过数据本身估计该参数进而确定应採取的数据变换形式,Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性,对许多实际数据都是行之有效的。
基本介绍
- 中文名:box-cox变换
- 外文名:Box-Cox transformation
- 性质:变换
- 所属学科:数学
- 属性:一种广义幂变换方法
- 相关方法:极大似然估计
简介
Box-Cox变换的一般形式为:
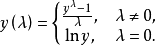
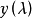
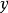

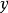

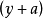

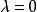
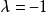
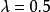


变换过程
Box-Cox变换是对回归因变数Y的如下变换:
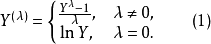


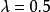
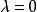
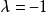
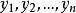
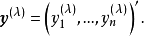

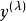
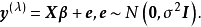
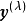

用极大似然方法来确定 ,由于
,由于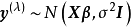 ,故对固定的
,故对固定的 ,
,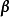 和
和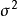 的似然函式为
的似然函式为

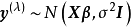

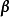
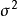
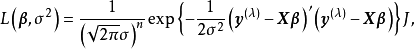
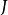
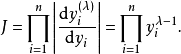

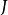
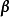
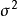

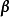
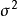
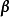
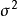
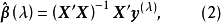

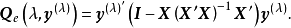
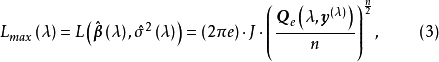


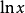
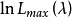

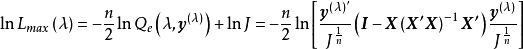
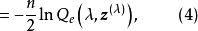
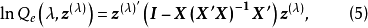

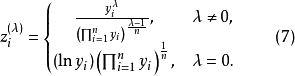

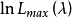







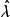
Box-Cox变换变换的具体步骤如下:
(1)对给定的 值,计算
值,计算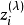 ,如果
,如果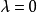 ,用式(6)计算,否则用式(7);
,用式(6)计算,否则用式(7);

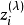
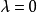
(2)利用式(5)计算残差平方和 ;
;

(3)对一系列的 值,重複上述步骤,得到相应的残差平方和
值,重複上述步骤,得到相应的残差平方和 的一串值,以
的一串值,以 为横轴,作出相应的曲线,用直观的方法,找出使
为横轴,作出相应的曲线,用直观的方法,找出使 达到最小值的点
达到最小值的点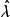 。
。




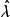
(4)利用式(2),求出 。
。

意义
Box-Cox变换的一个显着优点是通过求变换参数 来确定变换形式,而这个过程完全基于数据本身而无须任何先验信息,这无疑比凭经验或通过尝试而选用对数、平方根等变换方式要客观和精确。
来确定变换形式,而这个过程完全基于数据本身而无须任何先验信息,这无疑比凭经验或通过尝试而选用对数、平方根等变换方式要客观和精确。

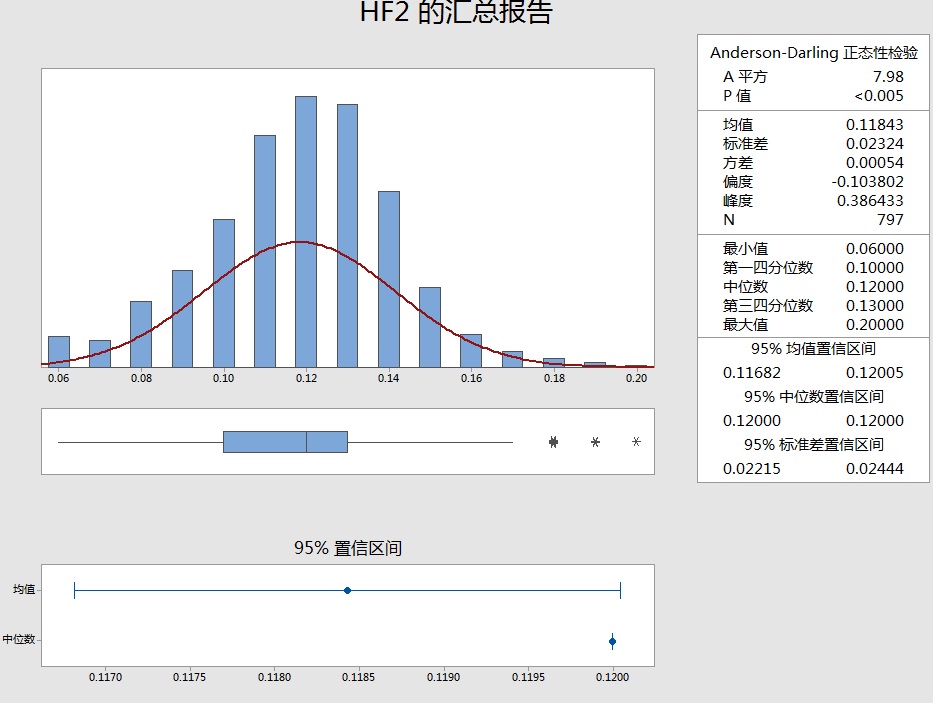
Box-Cox变换的目的是为了让数据满足线性模型的基本假定,即线性、正态性及方差齐性,然而经Box-Cox变换后数据是否同时满足了以上假定,仍需要考察验证。