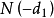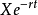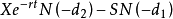B-S是两位经济学家BLACK、SCHOLES名字的缩写，为了纪念他们发现该模型而用他们的名字命名。 在二叉树的期权定价模型中，如果标的证券期末价格的可能性无限增多时，其价格的树状结构将无限延伸，从每个结点变化到下一个结点（上涨或下跌）的时间将不断缩短，如果价格随着时间周期的缩短，其调整的幅度也逐渐缩小的话，在极限的情况下，二叉树模型对欧式权证的定价就演变为关于权证定价理论的经典模型：B-S模型。
基本介绍
- 中文名：B-S模型
- 全称：期权定价模型
- 名字来源：BLACK、SCHOLES名字的缩写
- 目的：纪念他们发现该模型
成立条件
任何一个模型都是基于一定的市场假设的，Black-Scholes模型的基本假设有以下几点：
（1）在期权寿命期内，买方期权标的股票不发放股利，也不做其他分配；
（2）股票或期权的买卖没有交易成本；
（3）短期的无风险利率是已知的，并且在寿命期内保持不变；
（4）任何证券购买者都能以短期的无风险利率借得任何数量的资金；
（5）允许卖空，卖空者将立即得到所卖空股票当天价格的资金；
（6）看涨期权只能在到期日执行；
（7）所有证券交易都是连续发生的，股票价格随机游走。
计算方法
根据假设和数学推断，欧式认购期权价格的计算公式为：
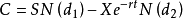
C——看涨 期权的当前价值；
X——期权的执行价格；
S——标的股票的当前价格；
t——期权到期日前的时间（年）；
r——连续複利的年度无风险利率；
N(d)——标準常态分配中离差小于d的机率；
e——自然对数的底数，约等于2.7183
对于该公式，我们可以从两个角度进行理解。
第一个角度根据定价原理，该模型可以看作两部分，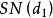
和
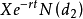，正好理解为一个投资组合的两个组成部分，即
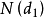份正股和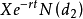 元的无息贷款的组合。也就是说，在权证未到期前的任何时刻，一份认购权证的价值与N(d1)份正股和 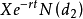元的无息贷款的组合价值相同。
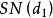
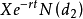
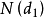
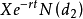
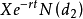
第二个角度是从权证的到期收益来理解模型，权证的价值由其到期日能够给持有者带来的收益决定。但是到期时正股价格不确定，因此权证的收益也难以确定。假设到期时正股价格为S，则到期时认购权证的价格为S-X。那幺在到期前的任一时刻t,要想知道认购权证的价格，我们就需要推算认购权证到期时正股价为S的机率，同时将行权价格按一定的贴现率折算为时刻t的现值。因此，认购权证的定价模型可以理解为在任一时刻t,认购权证到期时正股价格为S的机率为N(d1)，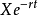
为行权价格在时刻t的现值，N(d2)为机率。因此，在任一时刻t,认购权证给投资者带来的收益即为
。
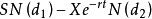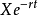
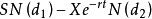
在得出了欧式认购权证的价格之后，很容易得出欧式认沽权证价格的计算公式，即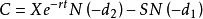
同样，我们也可以从两个不同的角度来直观理解认沽权证的B-S定价公式。
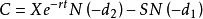
第一个角度是把认沽权证看作是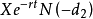
元无息存款与卖出
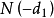份正股的组合。也就是说，在任一时刻，一份认沽权证的价值与卖出 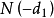份正股并同时存入 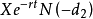元的无息存款的价值相同。
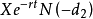
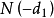
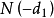
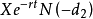
从另一个角度看，假设到期时正股价格为S元，则到期时认沽权证的价格为X-S元。认沽权证的B-S定价模型可以理解为在任一时刻t,认沽权证到期时正股价格为S的机率为 ，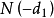
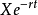为行权价格在时刻t的现值，因此，在任一时刻t,认沽权证能够给投资者带来的收益即为
。
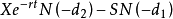