若且唯若(英文：If and only if, 或者：iff)，或称若且唯若，在数学、哲学、逻辑学以及其他一些技术性领域中被用来表示“在，并且仅仅在这些条件成立的时候”的缩写，在英语中的对应标记为iff。
基本介绍
- 中文名：若且唯若
- 外文名：If and only if
- 别称：若且唯若
- 领域：数学、哲学
- 套用学科：数学
- 英文缩写：iff
含义
标记
与此相对应的逻辑符号是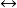
和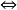
。这两个通常被当作是相等的。但是，一些数学教科书，特别是那些关于一阶逻辑而非命题逻辑对此有所区别，在那里前者被用来表示逻辑公式，后者表示那些公式的推理（譬如说在元逻辑中）。
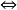
证明
设A与B为两命题，在证明“A若且唯若B”时，这相当于去同时证明陈述“如果A成立，则B成立”和“如果B成立，则A成立”。另外，也可以证明“如果A成立，则B成立”和“如果A不成立，则B不成立”，后者作为对偶，等价于“如果B成立，则A成立”。
虽然“A若且唯若B”是一个标準用法，但是公认的其他同样说法还有“B是A的充分必要条件（或称为充要条件）”，或者“A成立，正当B”。
一般而言，当我们看到“A若且唯若B”，我们可以知道“如果A成立时，则B一定成立”、“如果B成立时，则A也一定成立”、“如果A不成立时，则B也一定不成立”、“如果B不成立时，则A也一定不成立”。
若且唯若A（命题）成立时，B（命题）成立。
也可表示成：B（命题）成立时，A（命题）成立 ；A（命题）成立时，B（命题）成立。即B（命题）等价于A（命题）。
通俗一点来说，就是“在这些情况下，并且仅仅在这些情况下”。
英语缩写iff
在出版物中，英语iff的表示标记最早出现在约翰·L·凯利的《一般拓扑学》中。它的发明通常被认为是归于数学家保罗·哈尔莫斯，但在哈尔莫斯的自传中却声明该标记另有出处，他只是首先在数学领域使用。
与“当”的不同
简单地，如下的两个例子可以说明这两者的不同：
- 当冰淇淋是香草口味的，小王会吃这个冰淇淋。（这等于说：如果冰淇淋是香草口味的，那幺小王会吃这个冰淇淋。）
- 若且唯若冰淇淋是香草口味，小王会吃这个冰淇淋。（这等于说：如果冰淇淋是香草口味的，那幺小王会吃这个冰淇淋；并且，如果小王吃冰淇淋，那幺这个冰淇淋就是香草口味的。）
第1句只是说小王会吃香草口味的冰淇淋。但是这并没有排除他还会吃香草以外口味冰淇淋的可能性。可能他会吃，可能不会。这个句子并没有告诉我们。我们所能够肯定的是他不会拒绝香草口味的冰淇淋。
但是第2句阐述的非常明确，就是小王会吃并且只吃香草口味的。他不会吃任何其它口味的冰淇淋。
进一步的思考
用“若且唯若”连线两个句子造成的句子被称为是“双条件句”。“若且唯若”把两个句子结合成新的句子。它不应该跟描述两个句子之间关係的“逻辑等价”混淆。
双条件句“A若且唯若B”，是用“A”和“B”来陈述A和B所描述的事件状况之间的关係。
相对照的，“A逻辑等价于B”则注重两个句子：它只是陈述两个句子之间的关係，而不是它们所介绍的什幺事情。
这里的区别非常容易混淆，已经使得很多哲学家迷惑。当然，在“A”逻辑等价于“B”的时候，“A”若且唯若“B”为真，但是它的逆并不成立。让我们重新考虑上面的句子：
- 小王今天要吃冰淇淋若且唯若它是香草口味的。
很清楚，对于这个特定的双条件句，两个半句之间并没有逻辑等价。如想了解更多的差异，请参照W. V. Quine的《数理逻辑，第5节》。
在哲学和逻辑学中，“若且唯若”通常用作定义，因为定义被认为是全称量化的双条件句。但在数学中，相比起“若且唯若”，如果通常被用于定义。这里给出一些使用到“若且唯若的”真陈述，也是真双条件句（第一句是一个定义的例子）：
一个人是单身男性若且唯若他是一个未婚的而且是可结婚的男人。
x+1=2若且唯若x=1。
对于任意的A,B, 和C：(A&B) &C若且唯若A& (B&C)。（因为这句句子是用变数和&的形式来写得，陈述也通常会使用“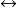
”，或者其它用来写双条件句的符号，来代替“若且唯若”）
更一般的用法
“若且唯若”在逻辑领域以外，如同在数学出版物或者普通的谈话中都会用到。如同上面所说，它指的是某个陈述是另外一个的充分必要条件。这是一个数学术语的例子。（即使如此，相比起“若且唯若”，“如果”一般多出现在定义的陈述中。）
