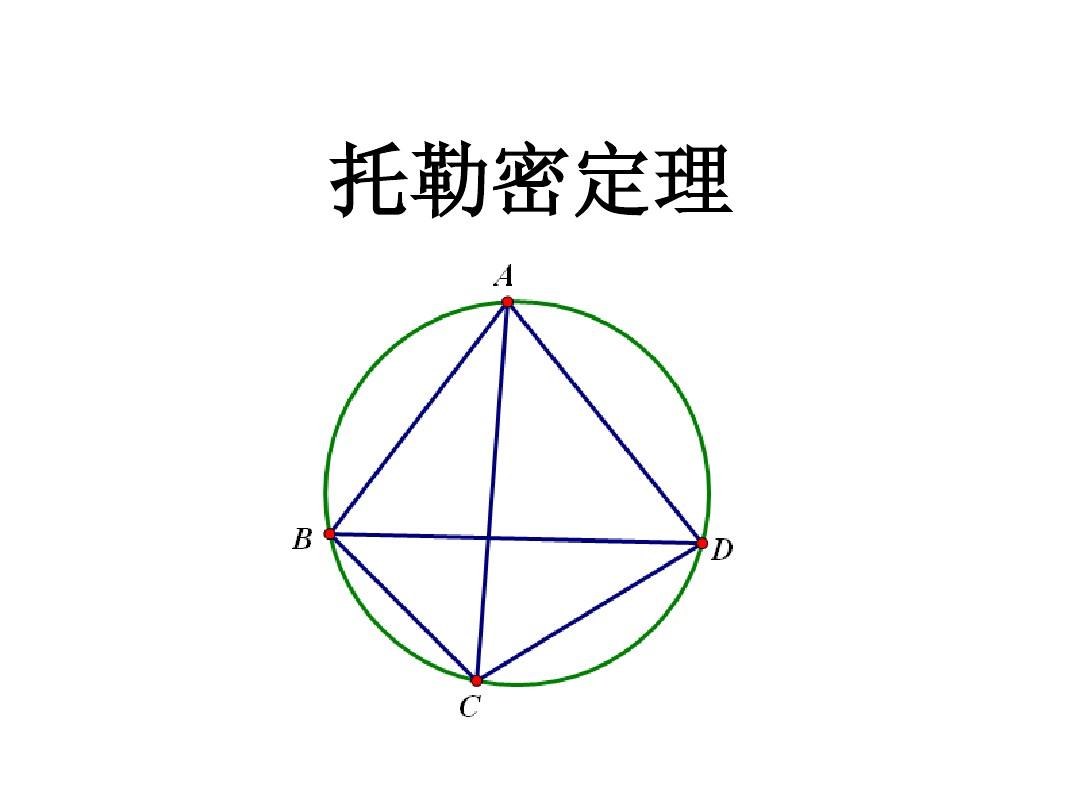
托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积,其推论是任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,而且当ABCD四点共圆时取等号。
基本介绍
- 中文名:广义托勒密定理
- 外文名:Ptolemy
- 内容:凸四边形对边乘积和≥对角线的积
- 提出者:托勒密
托勒密定理的推论:任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,而且当ABCD四点共圆时取等号。
证明如下:在四边形ABCD中,连线AC、BD,作∠ABE=∠ACD,∠BAE=∠CAD
则△ABE∽△ACD

∴ BE/CD=AB/AC,AB/AC=AE/AD
∴BE*AC=AB*CD ①,AB/AE=AC/AD
∵∠BAE=∠CAD
∴∠BAE+∠EAC=∠CAD+∠EAC
即∠BAC=∠DAE
又∵AB/AE=AC/AD,

∴△ABC∽△AED
∴BC/ED=AC/AD
∴ED*AC=AD*BC②
①+②,得
AC*(BE+ED)=AB*CD+AD*BC
又∵BE+ED≥BD
∴AC*BD≤AB*CD+AD*BC

从而命题得证,
且仅当E点落线上段BD上时,等号成立
此时∠ABD=∠ACD
∴ABCD四点共圆