在数学中，逐点收敛（或称简单收敛）描述的是一列函式向一个特定函式趋近的现象中的一种。简单来说，就是对定义域里的每一点，这个函式列在这点上的取值都趋于一个极限值。这时，被趋近的这个特定函式称作函式列的逐点极限。在各种收敛中，逐点收敛最为直观，容易想像，但不能很好地保持函式的一些重要性质，比如说连续性等等。
基本介绍
- 中文名：逐点收敛
- 外文名：Point-by-point convergence
- 分类：数理科学
定义
设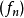
是一列拥有同样定义域的函式。
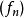逐点收敛若且唯若存在函式
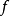，使得对定义域中的每个
，都有：
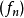
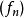
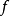
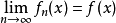
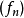
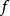
性质
与逐点收敛经常一起出现的一个概念是一致收敛。后者的定义如下：
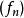
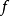
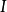
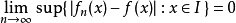
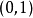
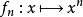
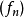
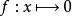
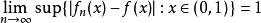
一致收敛能够保持函式列的连续性，但逐点收敛不能。例如，上述函式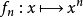
在闭区间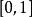
上连续，但是
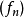逐点收敛到的函式 ，
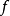在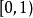
上取值为0，在1上取值为1，
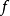不是连续函式。
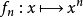
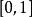
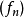
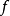
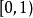
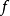
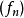
拓扑性质
逐点收敛也可以理解为由半範数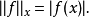
建立的拓扑。具有这种拓扑的函式组成的空间叫做逐点收敛空间。这个拓扑与乘积拓扑是等价的。如果
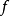的定义域和值域都是紧緻的，根据吉洪诺夫定理，这个空间也是紧緻的。
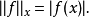
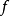
测度论
在测度理论中，对一个可测空间上的可测函式有几乎处处收敛的概念，也就是说几乎处处逐点收敛。叶戈罗夫定理说明，在有限测度的集合上几乎处处逐点收敛，意味着在稍微较小的集合上一致收敛。
